《微积分二》课程教学大纲
《微积分二》课程教学大纲
课程名称:微积分二
英文名称:Calculus 2
课程类型:公共平台课
总学时及学分:48学时 3学分
适应对象:本科一年级(经管类专业)
主要先修课程:微积分一
执行日期:2017年9月
一、 课程的性质与任务
性质:本课程是高等学校经济类、管理类各专业本科生重要的公共平台课,在微积分一的学习基础上对微积分知识更深入的学习,是后续学习其他课程的基础,并在经济活动、管理运作、社会生活等领域中有着广泛的应用。
任务:本课程以微积分基本理论问题为主线,主要向学生讲授微积分学中积分、级数、微分方程的基本概念和理论等内容,以及微积分知识在经济管理方面的应用。通过对微积分基本理论和方法的学习,培养学生的逻辑推理、量化思维能力,计算能力和创新意识。
二、 课程的教学目标
该课程的教学目标是:使学生初步掌握微积分二的基本理论和方法,通过学习定积分、多元函数微分学、无穷级数等课程内容,让学生学会用微积分的思想和方法来分析问题,同时提高学生的逻辑推理和空间想象能力,为后续专业课程的学习打下良好的基础。
三、 教学内容及其基本要求
(一) 定积分
1.积分的概念和性质
定积分定义 几何意义
2.微积分基本定理
变限积分与原函数 微积分基本定理
3.定积分的换元积分法和分部积分法
定积分的换元积分法 定积分的分部积分法
4.定积分的应用
平面图形的面积 立体的体积 定积分在经济学中的简单应用
5.反常积分初步
无穷限积分 瑕积分
教学基本要求:理解定积分的概念、几何意义、物理意义及定积分的性质;理解积分上限函数,并掌握其求导法则;掌握牛顿—莱布尼兹公式;掌握定积分的换元法和分部积分法;理解反常积分(广义积分)的概念,会计算反常积分,了解反常积分的敛散性。
教学重点:定积分的概念、几何意义及定积分的性质;积分上限的函数的求导法则;牛顿—莱布尼兹公式,定积分的换元法和分部积分法;反常积分(广义积分)的概念,简单的反常积分的收敛性。
教学难点:定积分的换元法和分部积分法;反常积分(广义积分)的概念及敛散性。
(二) 多元函数微积分学
1.预备知识
空间直角坐标系 空间直角坐标系中的向量 空间曲面与方程
2.多元函数的概念
多元函数的定义 二元函数的极限与连续性
3.方向导数,偏导数与全微分
方向导数与偏导数 全微分 梯度
4.多元复合函数与隐函数微分法
多元复合函数微分法 一阶全微分的形式不变性 隐函数微分法
5.高阶偏导数与高阶全微分
高阶偏导数 高阶全微分 二元函数的泰勒公式
6.多元函数的极值
多元函数的极值 条件极值
7.二重积分
二重积分的概念和性质 二重积分的计算
教学基本要求:了解多元函数的概念;理解二元函数的极限与连续的概念,了解有界闭区域上二元连续函数的性质;掌握多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数,会求全微分,了解隐函数存在定理,会求多元隐函数的偏导数;掌握多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,二元函数极值存在的充分条件,并会解决一些简单的应用问题;了解二重积分的概念与基本性质,掌握二重积分的计算方法。
教学重点:二元函数的极限与连续的概念;多元函数偏导数与全微分的概念,多元复合函数偏导数,全微分,隐函数存在定理,多元隐函数的偏导数;多元函数极值和条件极值的概念,二元函数极值存在的充分条件,二元函数的极值,拉格朗日乘数法求条件极值,简单多元函数的最大值和最小值;二重积分的概念与基本性质,二重积分的计算方法(直角坐标)。
教学难点:二元函数的极限与连续的概念,有界闭区域上二元连续函数的性质;多元复合函数一阶、二阶偏导数,全微分,隐函数存在定理,多元隐函数的偏导数;用拉格朗日乘数法求条件极值,多元函数的最大值和最小值;二重积分的计算方法(直角坐标)。
(三)无穷级数
1.常数项级数的概念和性质
常数项级数的概念 级数的基本性质
2.正项级数
比较判别法 比值判别法 根值判别法
3.任意项级数
莱布尼茨判别法
4.幂级数
函数项级数的概念 幂级数及其收敛性 幂级数的基本性质
教学基本要求:理解常数项级数收敛、发散以及收敛级数的和的概念,掌握级数的基本性质及收敛的必要条件;掌握几何级数与级数的收敛与发散的条件;掌握正项级数收敛性的比较判别法和比值判别法,会用根值判别法;掌握交错级数的莱布尼茨判别法;了解任意项级数绝对收敛与条件收敛的概念以及绝对收敛与收敛的关系;了解函数项级数的收敛域及和函数的概念;理解幂级数收敛半径的概念、并掌握幂级数的收敛半径、收敛区间及收敛域的求法。
教学重点:常数项级数的收敛与发散的概念;收敛级数的和的概念;级数的基本性质与收敛的必要条件;几何级数及其收敛性;正项级数收敛性的判别法、交错级数;任意项级数的绝对收敛与条件收敛;函数项级数的收敛域与和函数的概念;幂级数及其收敛半径、收敛区间(指开区间)和收敛域;幂级数的和函数、在其收敛区间内的基本性质;
初等函数的幂级数展开式。
教学难点:任意项级数的绝对收敛与条件收敛;函数项级数的收敛域与和函数的概念;幂级数及其收敛半径、收敛区间(指开区间)和收敛域;初等函数的幂级数展开式。
(四)微分方程初步
1.微分方程的基本概念
微分方程的定义 微分方程的解
2.一阶微分方程
可分离变量方程 齐次微分方程 一阶线性微分方程
3.二阶常系数线性微分方程
二阶常系数齐次线性方程 二阶常系数非齐次线性方程
4.微分方程在经济学中的应用
新产品的推广模型 价格调整模型 人才分配问题模型
教学基本要求:了解微分方程及其阶、解、通解、初始条件和特解等概念;掌握变量可分离的微分方程及一阶线性微分方程的解法;会解齐次微分方程,了解二阶常系数齐次线性微分方程的解法。
教学重点:常微分方程的基本概念;变量可分离的微分方程;齐次微分方程;一阶线性微分方程;二阶常系数齐次线性微分方程。
教学难点:一阶线性微分方程;二阶常系数齐次线性微分方程。
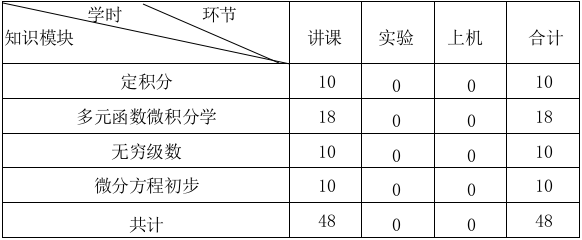
四、 各教学环节学时分配
五、教学建议
授课过程中,根据学情适当调整教学内容,对于偏难的证明内容可以省略,增加计算题的练习。
六、考核评价方法及要求
本课程以对学生微积分基础知识和应用能力的考核为主线,学生最终成绩采用平时成绩、测验成绩和期末考试成绩相结合的方式。
平时成绩是指任课教师通过记录每个学生上课出勤情况、课堂表现、作业情况等形式给出的成绩,占总评成绩的30%。
测验成绩是指在教学过程中通过对学生进行课堂测验而形成的成绩,测验共分4次,占总评成绩的20%。
期末考试作为一种定量测试手段,这种考试以评价学生综合应用微积分知识解决实际问题的能力为主,期末考试成绩占总评成绩的50%。
七、教材与主要教学参考资源
教材
1.朱来义:微积分,第三版,北京: 高等教育出版社,2009
参考资料
1.龚德恩:经济数学基础(微积分 第四版),成都: 四川人民出版社,2005
2.朱来义:微积分中典型例题分析与习题,第二版,北京: 高等教育出版社, 2009
3.王龙:微积分基础,华东理工大学出版社,2015
4.李红英:微积分同步辅导与习题全解,华东理工大学出版社,2015
5.杨淑辉,陈文英,卢立才:微积分,科学出版社有限责任公司,2016
6.邹彪:经济数学——微积分,西安电子科技大学出版社,2016
7.高源:经济数学——微积分同步辅导及习题讲解,第三版,水利水电出版社,2017
制定者:王文丽 2017年8月
审核者:张 曼 2017年8月
批准者:刘金宪 2017年8月